Understanding Signed and Unsigned Numbers in VBA

Whole decimal numbers can be represented in binary as either unsigned or signed types.

Unsigned Number Types in VBA

• Byte: 8-bit unsigned number from 0 to 255

Signed Number Types in VBA

• Integer: 16-bit signed number from -32,768 to 32,767
• Long: 32-bit signed number from -2,147,483,648 to 2,147,483,647
• LongLong: 64-bit signed number from -9,223,372,036,854,775,808 to 9,223,372,036,854,775,807

Note that the LongLong type is only available in 64-bit VBA.

Representing Numbers

Until we get quantum computing, we need to remember that everything in programming ultimately breaks down to ones and zeroes.

My favorite way to explore the relationship between the decimal, hexadecimal, and binary representations of a number is with the Programmer mode of the built-in Calculator utility in Windows 10.

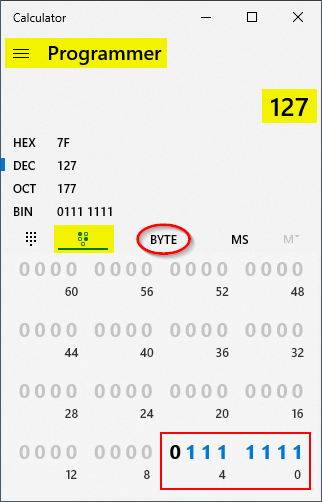
As the screenshot above shows, the number 127 is represented in binary as seven ones (1111111).  Each "1" represents a power of two: 64+32+16+8+4+2+1.  To represent 255, we add an eighth "1" to our binary number to get 11111111.  

As I listed at the top of this article, the VBA Byte data type is an 8-bit (eight ones or zeroes) unsigned number.  That means that all eight bits represent powers of two.  

The numbers in the Win 10 programmer's calculator are always signed numbers.  That means that the leading bit indicates whether the number is positive ("0") or negative ("1").  Thus, when we toggle on the eighth-bit for a BYTE-sized number in the programmer calculator, it evaluates to -1 instead of 255:

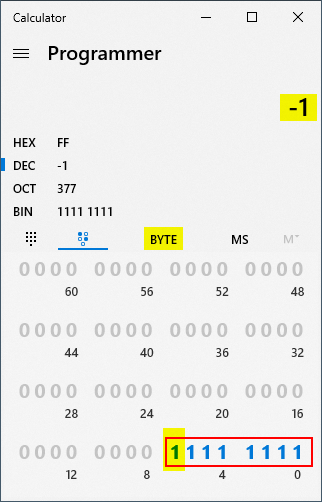
WORD to Your Mother

A group of 16 bits is called a WORD (WORD is not a VBA data type).  If we click on the text "BYTE" in the Programmer calculator, we can cycle through each different grouping of bits:

• BYTE: 8 bits
• WORD: 16 bits
• DWORD: 32 bits (a double word)
• QWORD: 64 bits (a quadruple word)

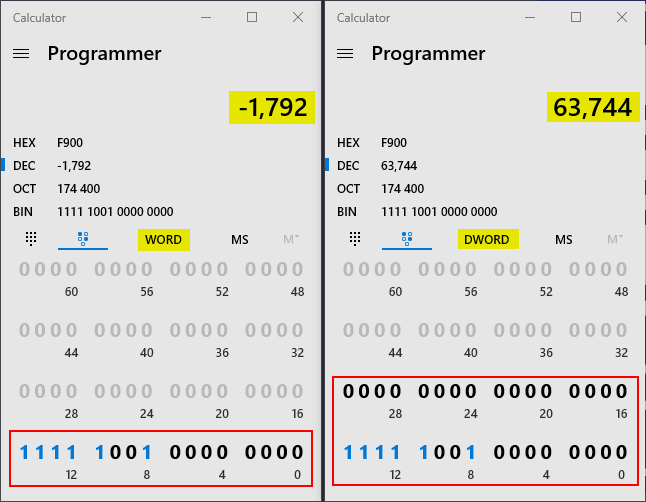
Without changing any of the bits in the calculator, we can change the decimal representation from -1 to 255 by simply switching from an 8-bit signed number to a 16-bit signed number:

Integer and Long

The same phenomenon happens as we continue to move up to larger and larger data types.

For example, the hex number F900 evaluates to -1,792 when converted to a 16-bit signed integer, but 63,744 when converted to a 32-bit signed integer:

Converting Among Long, Integer, and Hex in VBA

To represent a hexadecimal number in VBA, we can use a leading ampersand plus the letter "H":&h

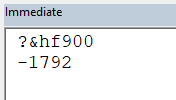
When VBA evaluates a hexadecimal number, it attempts to fit it into the Integer datatype if possible:

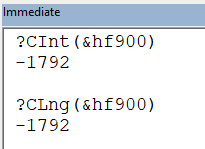
If we use the literal hexadecimal values, we have no control over which datatype VBA will choose to use.  We cannot force a literal hex value to be converted to a Long if it will fit in 16 or fewer bits: ^{(not quite true; see update below)}

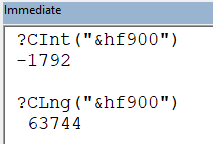
However, if–instead of a hexadecimal literal–we use a hexadecimal string, then we *CAN* force a conversion to Long:

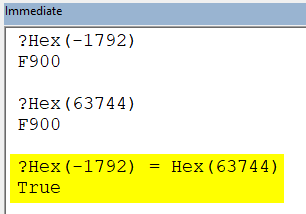
Finally, we can use the VBA Hex function to convert either decimal value back to the same original hex string:

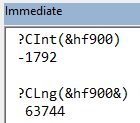
UPDATE [2023-02-14]: As Mark Johnstone points out in the comments below, the following line is not true:

We cannot force a literal hex value to be converted to a Long if it will fit in 16 or fewer bits

In fact, we can force a literal value to be a Long by appending the Long type suffix, which is an ampersand (&):

Thanks, Mark!

Image by Pexels from Pixabay