Intermediate

How to Construct a Bit Mask in VBA

What's the safest way to construct a bit mask in VBA? Your preferred approach may be more dangerous than you realize.

Mike Wolfe

Aug 16, 2021 • 6 min read

tl;dr: Use OR not +

Bit masks are a useful way to pass multiple boolean values to a routine, especially when those values are mostly false. An example most VBA developers are familiar with is the buttons argument of the MsgBox function:

Numeric expression that is the sum of values specifying the number and type of buttons to display, the icon style to use, the identity of the default button, and the modality of the message box. If omitted, the default value for buttons is 0.

Magic Numbers: The Worst Approach

You can combine the MsgBox constants to control the display of the message box dialog window.

Let's say you wanted to show a warning with Yes and No buttons where the second button is the default. You would combine the following three values:

4: Yes and No buttons
48: Warning message
256: Second button is default

If you add up the three numbers above–4 + 48 + 256–you get 308. So, you could pass the number 308 as the buttons argument:

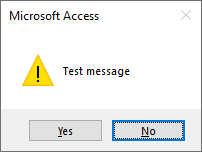
Of course, this would be terrible programming practice. The literal 308 is what's known as a "magic number" in programming.

Addition of Constants: A Big Improvement

Instead of passing 308 in literal form to the function, it's better to build up the number from its component MsgBox constants:

4: vbYesNo
48: vbExclamation
256: vbDefaultButton2

So, a better way to call the same message box is to add the constants as shown in the caption below:

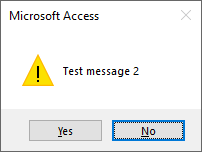
`MsgBox "Test message 2", vbYesNo + vbExclamation + vbDefaultButton2`

This is better than using magic numbers, but there's still room for improvement.

The problem is that we are using addition to combine the constants. When constructing a bit mask, it is always safer to use a bitwise OR operation.

The problem with using addition to build a bit mask

Let's say that we have the following convenience function:

'Returns True if user presses [Yes] button, False otherwise
Function UserConfirms(Options As VbMsgBoxStyle) As Boolean
    UserConfirms = (MsgBox("Are you sure?", vbYesNo + Options) = vbYes)
End Function

The intent of the function is to always show Yes and No buttons, but to allow the calling code to change the default button or the displayed icon (e.g., question mark, exclamation point, etc.).

We can call this function as shown in the caption below and it works just fine. The [Yes] and [No] buttons are shown, the second button is the default, and the icon is the Exclamation point.

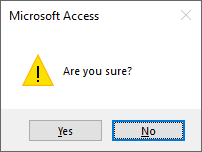
This works fine: `?UserConfirms(vbExclamation + vbDefaultButton2)`

But what happens if, when writing the calling code, we forget that the vbYesNo option is included within the UserConfirms function? Then, "just to be on the safe side", we also include the vbYesNo option when calling the code. Here's what happens:

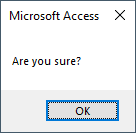
Uh-oh, this doesn't look right: `?UserConfirms(vbExclamation + vbDefaultButton2 + vbYesNo)`

What happened? The vbYesNo constant got added in twice. The calling code passed in vbExclamation (48) + vbDefaultButton2 (256) + vbYesNo (4) for a total of 308. The UserConfirms function then took the 308 and added it to the vbYesNo (4) constant for a total of 312.

Bitwise OR Operations: A Safe Way to Build Bit Masks

We can avoid the problem above if we replace the addition operation inside the UserConfirms function with a bitwise OR operation:

Function UserConfirms_OR(Options As VbMsgBoxStyle) As Boolean
    UserConfirms_OR = (MsgBox("Are you sure?", vbYesNo Or Options) = vbYes)
End Function

Replacing the addition operator with the Or operator is a safer way to build a bit mask.

It does not matter if we include the vbYesNo constant when we call the function now. The bitwise OR operation prevents it from being "double-counted."

We can include the vbYesNo option and everything still works: `?UserConfirms_OR(vbExclamation + vbDefaultButton2 + vbYesNo)`. Of course, if we are building good habits, we should probably call the function like so: `?UserConfirms_OR(vbExclamation Or vbDefaultButton2 Or vbYesNo)`.

Visualizing the Bit Mask

The above explanation is difficult to follow if you are unfamiliar with the concept of bit masks.

Hopefully, the graphic below will clarify what's going on a bit (pun intended).

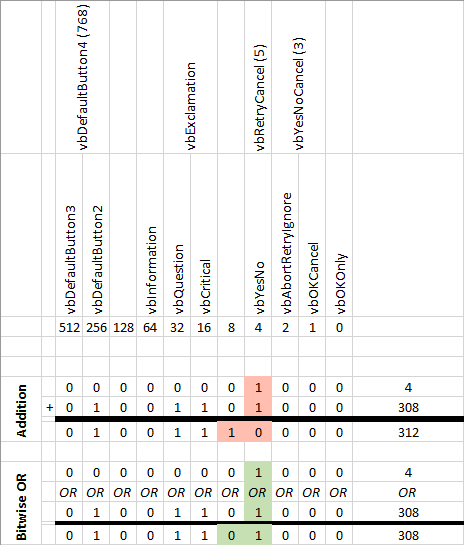
A visualization of the difference between standard addition and a bitwise OR operation.

The top part of the graphic simply maps the MsgBox constants to their corresponding values.

The first row of numbers represent the binary values of their respective columns. This is analogous to decimal notation where the first digit represents the "ones" column, the second digit represents the "tens" column, the third digit represents the "hundreds" column, etc. Except, in the case of binary, the first digit represents the "ones" column, the second digit represents the "twos" column, the third digit represents the "fours" column, etc.

The bottom half of the graphic shows the two calculations: first, the basic addition and second, the bitwise OR operation.

In the basic addition section, we add 4 plus 308 and get 312. More importantly, though, the value in the "fours" column becomes 0 as the number in the "eights" column becomes 1. The binary math is just like decimal math: one (1) plus one (1) equals two (10), so we put zero in the "fours" column and carry the one over to the "eights" column. (This is the equivalent of "five (5) plus five (5) equals ten (10), put zero in the column and carry the one.") The key numbers are highlighted in red.

If instead, we perform a bitwise OR operation, 4 OR 308 equals 308. That's because of how the two 1's are handled in the "fours" column. You never "carry" numbers when doing a bitwise OR. If either or both numbers are 1, the OR'ed result is 1. The OR'ed result is only 0 if both numbers are 0. The numbers highlighted in green demonstrate this concept.

Revisiting the Examples

The message box buttons are determined by the value of the first three binary digits; the "ones", "twos", and "fours" columns combine to create values between 0 (vbOKOnly) and 5 (vbRetryCancel).

In the addition example, the result of adding 4 + 4 is that these first three columns are all set to 0 (refer to the 312 row). Since a value of 0 corresponds with vbOKOnly, we see the [OK] button only in that example:

Addition is BAD: `?UserConfirms(vbExclamation + vbDefaultButton2 + vbYesNo)`

In the bitwise OR example, though, the result of OR'ing 4 with 4 is 4. Thus, the value in the first three columns is 4, which corresponds to vbYesNo. When we call the OR version of UserConfirms, we see both a [Yes] and a [No] button: